Содержание

1. Введение
2. Ракетные двигатели
3. Космические ракеты
4. Космические скорости
5. Законы Кеплера
6. Орбиты

Введение

Слово космос является синонимом слова Вселенная. Часто космос разделяют несколько условно на ближний, который возможно исследовать в настоящее время при помощи искусственных спутников Земли, космических аппаратов, межпланетных станций и других средств, и дальний - все остальное, несоизмеримо большее. По сути дела, под ближним космосом понимается Солнечная система, а под дальним - необъятные просторы звезд и галактик.

Буквальный смысл слова «космонавтика», представляющего собой сочетание двух греческих слов - «плавание во Вселенной». В обычном употреблении это слово означает совокупность различных отраслей науки и техники, обеспечивающих исследование и освоение космического пространства и небесных тел с помощью космических летательных аппаратов - искусственных спутников, автоматических станций различного назначения, пилотируемых космических кораблей.

Космонавтика, или, как ее иногда называют, астронавтика, объединяет в себе полеты в космическое пространство, совокупность отраслей науки и техники, служащих для исследования и использования космического пространства в интересах нужд человечества с использованием различных космических средств. Началом космической эры человечества считается 4 октября 1957 г. - дата, когда в Советском Союзе был запущен первый искусственный спутник Земли.

Теория космических полетов, представлявших давнюю мечту человечества, превратилась в науку в результате основополагающих трудов великого русского ученого Константина Эдуардовича Циолковского. Им были изучены основные принципы баллистики ракет, предложена схема жидкостного ракетного двигателя, установлены закономерности, определяющие реактивную силу двигателя. Так же были предложены схемы космических кораблей и даны широко вошедшие сейчас в практику принципы конструирования ракет. В течение продолжительного времени, до того момента, когда идеи, формулы и чертежи энтузиастов и ученых стали в конструкторских бюро и в цехах заводов превращаться в объекты, изготовленные «в металле», теоретический фундамент космонавтики покоился на трех китах: 1) теории движения космических аппаратов; 2) ракетной технике; 3) совокупности астрономических знаний о Вселенной. Впоследствии в недрах космонавтики зародился широкий цикл новых научно-технических дисциплин, таких, как теория систем управления космическими объектами, космическая навигация, теория космических систем связи и передачи информации, космическая биология и медицина и т. д. Сейчас, когда нам трудно представить себе космонавтику без этих дисциплин, полезно вспомнить о том, что теоретические основы космонавтики закладывались К. Э. Циолковским в то время, когда производились лишь первые опыты над использованием радиоволн и радио не могло считаться средством связи в космосе.

В течение многих лет в качестве средства связи всерьез рассматривалась сигнализация с помощью лучей солнечного света, отражаемых в сторону Земли зеркалами, находящимися на борту межпланетного корабля. Сейчас, когда мы привыкли не удивляться ни прямому телевизионному репортажу с поверхности Луны, ни полученным по радио фотографиям, сделанным вблизи Юпитера или на поверхности Венеры, в это трудно поверить. Поэтому можно утверждать, что теория космической связи, несмотря на всю свою важность, не является все же главным звеном в цепи космических дисциплин. Таким главным звеном служит теория движения космических объектов. Именно ее можно считать теорией космических полетов. Специалисты, занимающиеся этой наукой, сами называют ее по-разному: прикладная небесная механика, небесная баллистика, космическая баллистика, космодинамика, механика космического полета, теория движения искусственных небесных тел. Все эти названия имеют один и тот же смысл, точно выражаемый последним термином. Космодинамика, таким образом, является частью небесной механики - науки, изучающей движение любых небесных тел, как естественных (звезды, Солнце, планеты, их спутники, кометы, метеорные тела, космическая пыль), так и искусственных (автоматические космические аппараты и пилотируемые корабли). Но есть нечто, выделяющее космодинамику из небесной механики. Родившаяся в лоне небесной механики космодинамика пользуется ее методами, но не умещается в ее традиционных рамках.

Существенное отличие прикладной небесной механики от классической заключается в том, что вторая не занимается и не может заниматься выбором орбит небесных тел, в то время как первая занимается отбором из огромного числа возможных траекторий достижения того или иного небесного тела определенной траектории, которая учитывает многочисленные, зачастую противоречивые требования. Главное требование - минимальность скорости, до которой разгоняется космический аппарат на начальном активном участке полета и соответственно минимальность массы ракеты-носителя или орбитального разгонного блока (при старте с околоземной орбиты). Это обеспечивает максимальную полезную нагрузку и, следовательно, наибольшую научную эффективность полета. Учитываются также требования простоты управления, условий радиосвязи (например, в момент захода станции за планету при ее облете), условий научных исследований (посадка на дневной или ночной стороне планеты) и т. п. Космодинамика предоставляет в распоряжение проектировщиков космической операции методы оптимального перехода с одной орбиты на другую, способы исправления траектории. В поле ее зрения находится неведомое классической небесной механике орбитальное маневрирование. Космодинамика представляет собой фундамент общей теории космического полета (подобно тому как аэродинамика представляет собой фундамент теории полета в атмосфере самолетов, вертолетов, дирижаблей и других летательных аппаратов). Эту свою роль космодинамика делит с ракетодинамикой - наукой о движении ракет. Обе науки, тесно переплетаясь, лежат в основе космической техники. Обе они являются разделами теоретической механики, которая сама представляет собой обособившийся раздел физики. Будучи точной наукой, космодинамика использует математические методы исследования и требует логически стройной системы изложения. Недаром основы небесной механики были разработаны после великих открытий Коперника, Галилея и Кеплера именно теми учеными, которые внесли величайший вклад в развитие математики и механики. Это были Ньютон, Эйлер, Клеро, Даламбер, Лагранж, Лаплас. И в настоящее время математика помогает решению задач небесной баллистики и в свою очередь получает толчок в своем развитии благодаря тем задачам, которые космодинамика перед ней ставит.

Классическая небесная механика была чисто теоретической наукой. Ее выводы находили неизменное подтверждение в данных астрономических наблюдений. Космодинамика привнесла в небесную механику эксперимент, и небесная механика впервые превратилась в экспериментальную науку, подобную в этом отношении, скажем, такому разделу механики, как аэродинамика. На смену поневоле пассивному характеру классической небесной механики пришел активный, наступательный дух небесной баллистики. Каждое новое достижение космонавтики - это вместе с тем свидетельство эффективности и точности методов космодинамики. Космодинамика делится на две части: теорию движения центра масс космического аппарата (теорию космических траекторий) и теорию движения космического аппарата относительно центра масс (теорию «вращательного движения»).

наверх ^

Ракетные двигатели

Основным и почти единственным средством передвижения в мировом пространстве является ракета, которая для этой цели была впервые предложена в 1903 г. К. Э. Циолковским. Законы ракетного движения представляют собой один из краеугольных камней теории космического полета.

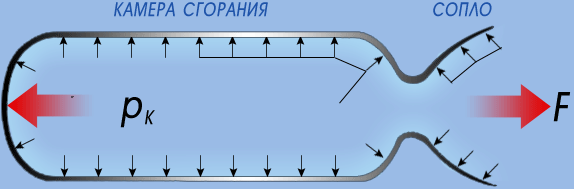
Космонавтика обладает большим арсеналом ракетных двигательных систем, основанных на использовании различных видов энергии. Но во всех случаях ракетный двигатель осуществляет одну и ту же задачу: он тем или иным способом выбрасывает из ракеты некоторую массу, запас которой (так называемое рабочее тело) находится внутри ракеты. На выбрасываемую массу со стороны ракеты действует некоторая сила, и согласно третьему закону механики Ньютона - закону равенства действия и противодействия - такая же сила, но противоположно направленная, действует со стороны выбрасываемой массы на ракету. Эта последняя сила, приводящая ракету в движение, называется силой тяги. Интуитивно ясно, что сила тяги должна быть тем больше, чем большая масса в единицу времени выбрасывается из ракеты и чем больше скорость, которую удается сообщить выбрасываемой массе.

Простейшая схема устройства ракеты:

На данном этапе развития науки и техники существуют ракетные двигатели, основанные на разных принципах действия.

Термохимические ракетные двигатели.

Принцип действия термохимических (или просто химических) двигателей не сложен: в результате химической реакции (как правило, реакции горения) выделяется большое количество тепла и нагретые до высокой температуры продукты реакции, стремительно расширяясь, с большой скоростью истечения выбрасываются из ракеты. Химические двигатели относятся к более широкому классу тепловых (теплообменных) двигателей, в которых истечение рабочего тела осуществляется в результате его расширения посредством нагревания. Для таких двигателей скорость истечения в основном зависит от температуры расширяющихся газов и от их среднего молекулярного веса: чем больше температура и чем меньше молекулярный вес, тем больше скорость истечения. По этому принципу работают жидкостные ракетные двигатели, ракетные двигатели твердого топлива, воздушно-реактивные двигатели.

Ядерные тепловые двигатели.

Принцип действия этих двигателей почти не отличается от принципа действия химических двигателей. Разница заключается в том, что рабочее тело нагревается не за счет своей собственной химической энергии, а за счет «постороннего» тепла, выделяющегося при внутриядерной реакции. По этому принципу проектировались пульсирующие ядерные тепловые двигатели, ядерные тепловые двигатели на термоядерном синтезе, на радиоактивном распаде изотопов. Однако опасность радиоактивного заражения атмосферы и заключение договора о прекращении ядерных испытаний в атмосфере, в космосе и под водой, привели к прекращению финансирования упомянутых проектов.

Тепловые двигатели с внешним источником энергии.

Принцип их действия основан на получении энергии извне. По этому принципу проектируют гелиотермический двигатель, источником энергии которому служит Солнце. Концентрируемые с помощью зеркал солнечные лучи используются для непосредственного нагрева рабочего тела.

Электрические ракетные двигатели.

Этот обширный класс двигателей объединяет различные типы двигателей, которые очень интенсивно разрабатываются в настоящее время. Разгон рабочего тела до определенной скорости истечения производится за счет электрической энергии. Энергия получается от атомной или солнечной электростанции, находящейся на борту космического корабля (в принципе даже от химической батареи). Схемы разрабатываемых электрических двигателей чрезвычайно разнообразны. Это и электротермические двигатели, электростатические (ионные) двигатели, электромагнитные (плазменные) двигатели, электрические двигатели с забором рабочего тела из верхних слоев атмосферы.

наверх ^

Космические ракеты

Современная космическая ракета представляет собой сложное сооружение, состоящее из сотен тысяч и миллионов деталей, каждая из которых играет предназначенную ей роль. Но с точки зрения механики разгона ракеты до необходимой скорости всю начальную массу ракеты можно разделить на две части: 1) масса рабочего тела и 2) конечная масса, остающаяся после выброса рабочего тела. Эту последнюю часто называют «сухой» массой, так как рабочее тело в большинстве случаев представляет собой жидкое топливо. «Сухая» масса (или, если угодно, масса «пустой», без рабочего тела, ракеты) состоит из массы конструкции и массы полезной нагрузки. Под конструкцией следует понимать не только несущую конструкцию ракеты, ее оболочку и т. п., но и двигательную систему со всеми ее агрегатами, систему управления, включающую органы управления, аппаратуру навигации и связи, и т. п.,- одним словом, все то, что обеспечивает нормальный полет ракеты. Полезная нагрузка состоит из научной аппаратуры, радиотелеметрической системы, корпуса выводимого на орбиту космического аппарата, экипажа и системы жизнеобеспечения космического корабля и т. п. Полезная нагрузка - это то, без чего ракета может совершить нормальный полет.

Набору скорости ракеты благоприятствует то, что по мере истечения рабочего тела масса ракеты уменьшается, благодаря чему при неизменной тяге непрерывно растет реактивное ускорение. Но, к сожалению, ракета состоит не из одного лишь рабочего тела. По мере истечения рабочего тела освободившиеся баки, лишние части оболочки и т. д. начинают обременять ракету мертвым грузом, затрудняя ее разгон. Целесообразно в некоторые моменты отделять эти части от ракеты. Построенная таким образом ракета называется составной. Часто составная ракета состоит из самостоятельных ракет- ступеней (благодаря этому из отдельных ступеней можно составлять различные ракетные комплексы), соединенных последовательно. Но возможно и параллельное соединение ступеней, бок о бок. Наконец, существуют проекты составных ракет, в которых последняя ступень входит внутрь предыдущей, та заключена внутри предшествующей и т. д.; при этом ступени имеют общий двигатель и уже не являются самостоятельными ракетами. Существенный недостаток последней схемы заключается в том, что после отделения отработавшей ступени резко возрастает реактивное ускорение, так как двигатель остался прежним, тяга поэтому не изменилась, а разгоняемая масса ракеты резко уменьшилась. Это затрудняет точность наведения ракеты и предъявляет повышенные требования к прочности конструкции. При последовательном же соединении ступеней вновь включаемая ступень обладает меньшей тягой и ускорение не изменяется резким скачком. Пока работает первая ступень, мы можем рассматривать остальные ступени вместе с истинной полезной нагрузкой в качестве полезной нагрузки первой ступени. После отделения первой ступени начинает работать вторая ступень, которая вместе с последующими ступенями и истинной полезной нагрузкой образует самостоятельную ракету («первую субракету»). Для второй ступени все последующие ступени вместе с истинным полезным грузом играют роль собственной полезной нагрузки и т. д. Каждая субракета добавляет к уже имеющейся скорости собственную идеальную скорость, и в результате конечная идеальная скорость многоступенчатой ракеты складывается из суммы идеальных скоростей отдельных субракет.

Ракета является весьма «затратным» транспортным средством. Ракеты-носители космических аппаратов «транспортируют», главным образом, топливо, необходимое для работы их двигателей и собственную конструкцию, состоящую в основном из топливных контейнеров и двигательной установки. На долю полезной нагрузки приходится лишь малая часть (1,5-2,0%) стартовой массы ракеты.

Составная ракета позволяет более рационально использовать ресурсы за счет того, что в полете ступень, выработавшая свое топливо, отделяется, и остальное топливо ракеты не тратится на ускорение конструкции отработавшей ступени, ставшей ненужной для продолжения полета.

Варианты компоновки ракет. Слева направо:

1. Одноступенчатая ракета.
2. Двухступенчатая ракета с поперечным разделением.
3. Двухступенчатая ракета с продольным разделением.
4. Ракета с внешними топливными емкостями, отделяемыми после исчерпания топлива в них.

Конструктивно многоступенчатые ракеты выполняются c поперечным или продольным разделением ступеней.

При поперечном разделении ступени размещаются одна над другой и работают последовательно друг за другом, включаясь только после отделения предыдущей ступени. Такая схема дает возможность создавать системы, в принципе, с любым количеством ступеней. Недостаток ее заключается в том, что ресурсы последующих ступеней не могут быть использованы при работе предыдущей, являясь для нее пассивным грузом.

При продольном разделении первая ступень состоит из нескольких одинаковых ракет (на практике, от двух до восьми), располагающихся вокруг корпуса второй ступени симметрично, чтобы равнодействующая сил тяги двигателей первой ступени была направлена по оси симметрии второй, и работающих одновременно. Такая схема позволяет работать двигателю второй ступени одновременно с двигателями первой, увеличивая таким образом суммарную тягу, что особенно нужно во время работы первой ступени, когда масса ракеты максимальна. Но ракета с продольным разделением ступеней может быть только двухступенчатой.

Существует и комбинированная схема разделения - продольно-поперечная, позволяющая совместить преимущества обеих схем, при которой первая ступень разделяется со второй продольно, а разделение всех последующих ступеней происходит поперечно. Пример такого подхода - отечественный носитель "Союз".

Уникальную схему двухступенчатой ракеты с продольным разделением имеет космический корабль Спейс Шаттл, первая ступень которого состоит из двух боковых твердотопливных ускорителей, на второй ступени часть топлива содержится в баках орбитера (собственно многоразового корабля), а большая часть - в отделяемом внешнем топливном баке. Сначала двигательная установка орбитера расходует топливо из внешнего бака, а когда оно будет исчерпано, внешний бак сбрасывается и двигатели продолжают работу на том топливе, которое содержится в баках орбитера. Такая схема позволяет максимально использовать двигательную установку орбитера, которая работает на всем протяжении вывода корабля на орбиту.

При поперечном разделении ступени соединяются между собой специальными секциями - переходниками - несущими конструкциями цилиндрической или конической формы (в зависимости от соотношения диаметров ступеней), каждый из которых должен выдерживать суммарный вес всех последующих ступеней, помноженный на максимальное значение перегрузки, испытываемой ракетой на всех участках, на которых данный переходник входит в состав ракеты. При продольном разделении на корпусе второй ступени создаются силовые бандажи (передний и задний), к которым крепятся блоки первой ступени.

Элементы, соединяющие части составной ракеты, сообщают ей жесткость цельного корпуса, а при разделении ступеней должны практически мгновенно освобождать верхнюю ступень. Обычно соединение ступеней выполняется с помощью пироболтов. Пироболт - это крепежный болт, в стержне которого рядом с головкой создается полость, заполняемая бризантным взрывчатым веществом с электродетонатором. При подаче импульса тока на электродетонатор происходит взрыв, разрушающий стержень болта, в результате чего его головка отрывается. Количество взрывчатки в пироболте тщательно дозируется, чтобы, с одной стороны, гарантированно оторвать головку, а, с другой - не повредить ракету. При разделении ступеней на электродетонаторы всех пироболтов, соединяющих разделяемые части, одновременно подается импульс тока, и соединение освобождается.

Далее ступени должны быть разведены на безопасное расстояние друг от друга. (Запуск двигателя высшей ступени вблизи низшей может вызвать прогар ее топливной емкости и взрыв остатков топлива, который повредит верхнюю ступень, или дестабилизирует ее полет.) При разделении ступеней в атмосфере для их разведения может быть использована аэродинамическая сила встречного потока воздуха, а при разделении в пустоте иногда используются вспомогательные небольшие твердотопливные ракетные двигатели.

На жидкостных ракетах эти же двигатели служат и для того, чтобы «осадить» топливо в баках верхней ступени: при выключении двигателя низшей ступени ракета летит по инерции, в состоянии свободного падения, при этом жидкое топливо в баках находится во взвешенном состоянии, что может привести к сбою при запуске двигателя. Вспомогательные двигатели сообщают ступени небольшое ускорение, под действием которого топливо «оседает» на днища баков.

Увеличение числа ступеней дает положительный эффект только до определенного предела. Чем больше ступеней, тем больше суммарная масса переходников, а также двигателей, работающих лишь на одном участке полета, и, в какой-то момент, дальнейшее увеличение числа ступеней становится контрпродуктивным. В современной практике ракетостроения более четырех ступеней, как правило, не делается.

При выборе числа ступеней важное значение имеют также вопросы надежности. Пироболты и вспомогательные твердотопливные ракетные двигатели - элементы одноразового действия, проверить функционирование которых до старта ракеты невозможно. Между тем, отказ только одного пироболта может привести к аварийному завершению полета ракеты. Увеличение числа одноразовых элементов, не подлежащих проверке функционирования, снижает надежность всей ракеты в целом. Это также заставляет конструкторов воздерживаться от слишком большого количества ступеней.

наверх ^

Космические скорости

Чрезвычайно важно отметить, что скорость, развиваемая ракетой (а вместе с ней и всем космическим летательным аппаратом) на активном участке пути, т. е. на том сравнительно коротком участке, пока работает ракетный двигатель, должна быть достигнута очень и очень высокая.

Поместим мысленно нашу ракету в свободное пространство и включим ее двигатель. Двигатель создал тягу, ракета получила какое-то ускорение и начала набирать скорость, двигаясь по прямой линии (если сила тяги не меняет своего направления). Какую скорость приобретет ракета к моменту, когда ее масса уменьшится от начальной m₀ до конечной величины m_k? Если допустить, что скорость истечения w вещества из ракеты неизменна (это довольно точно соблюдается в современных ракетах), то ракета разовьет скорость v, выражающуюся формулой Циолковского, определяющая скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил:

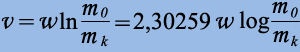
где ln обозначает натуральный, а log – десятичный логарифмы

Скорость, вычисляемая по формуле Циолковского, характеризует энергетические ресурсы ракеты. Она называется идеальной. Мы видим, что идеальная скорость не зависит от секундного расхода массы рабочего тела, а зависит только от скорости истечения w и от числа z = m₀/m_k, называемого отношением масс или числом Циолковского.

Существует понятие так называемых космических скоростей: первой, второй и третьей. Первой космической скоростью называется такая скорость, при достижении которой тело (космический аппарат), запущенное с Земли, может стать ее спутником. Если не учитывать влияния атмосферы, то непосредственно над уровнем моря первая космическая скорость составляет 7,9 км/с и с увеличением расстояния от Земли уменьшается. На высоте 200 км от Земли она равна 7,78 км/с. Практически первая космическая скорость принимается равной 8 км/с.

Для того чтобы преодолеть притяжение Земли и превратиться, например, в спутник Солнца или достигнуть какой-нибудь другой планеты Солнечной системы, запускаемое с Земли тело (космический аппарат) должно достигнуть второй космической скорости, принимаемой равной 11,2 км/с.

Третьей космической скоростью у поверхности Земли телу (космическому аппарату) необходимо обладать в том случае, когда требуется, чтобы оно могло преодолеть притяжение Земли и Солнца и покинуть Солнечную систему. Третья космическая скорость принимается равной 16,7 км/с.

Космические скорости по своему значению огромны. Они в несколько десятков раз превышают скорость звука в воздухе. Только из этого ясно видно, какие сложные задачи стоят в области космонавтики.

Почему же космические скорости такие огромные и почему космические аппараты не падают на Землю? Действительно, странно: Солнце огромными силами тяготения удерживает около себя Землю и все другие планеты Солнечной системы, не дает им улететь в космическое пространство. Странно, казалось бы, то, что Земля около себя удерживает Луну. Между всеми телами действуют силы тяготения, но не падают планеты на Солнце потому, что находятся в движении, в этом-то и секрет.

Все падает вниз, на Землю: и капли дождя, и снежинки, и сорвавшийся с горы камень, и опрокинутая со стола чашка. А Луна? Она вращается вокруг Земли. Если бы не силы тяготения, она улетела бы по касательной к орбите, а если бы она вдруг остановилась, то упала бы на Землю. Луна, вследствие притяжения Земли, отклоняется от прямолинейного пути, все время как бы "падая" на Землю.

Движение Луны происходит по некоторой дуге, и пока действует гравитация, Луна на Землю не упадет. Так же и с Землей - если бы она остановилась, то упала бы на Солнце, но этого не произойдет по той же причине. Два вида движения - одно под действием силы тяготения, другое по инерции - складываются и в результате дают криволинейное движение.

Закон всемирного тяготения, удерживающий в равновесии Вселенную, открыл английский ученый Исаак Ньютон. Когда он опубликовал свое открытие, люди говорили, что он сошел с ума. Закон тяготения определяет не только движение Луны, Земли, но и всех небесных тел в Солнечной системе, а также искусственных спутников, орбитальных станций, межпланетных космических кораблей.

наверх ^

Законы Кеплера

Прежде чем рассматривать орбиты космических аппаратов, рассмотрим законы Кеплера, которые их описывают.

Иоганн Кеплер обладал чувством прекрасного. Всю свою сознательную жизнь он пытался доказать, что Солнечная система представляет собой некое мистическое произведение искусства. Сначала он пытался связать ее устройство с пятью правильными многогранниками классической древнегреческой геометрии. (Правильный многогранник - объемная фигура, все грани которой представляют собой равные между собой правильные многоугольники.) Во времена Кеплера было известно шесть планет, которые, как полагалось, помещались на вращающихся «хрустальных сферах». Кеплер утверждал, что эти сферы расположены таким образом, что между соседними сферами точно вписываются правильные многогранники. Между двумя внешними сферами - Сатурна и Юпитера - он поместил куб, вписанный во внешнюю сферу, в который, в свою очередь, вписана внутренняя сфера; между сферами Юпитера и Марса - тетраэдр (правильный четырехгранник) и т. д. Шесть сфер планет, пять вписанных между ними правильных многогранников - казалось бы, само совершенство?

Увы, сравнив свою модель с наблюдаемыми орбитами планет, Кеплер вынужден был признать, что реальное поведение небесных тел не вписывается в очерченные им стройные рамки. Единственным пережившим века результатом того юношеского порыва Кеплера стала модель Солнечной системы, собственноручно изготовленная ученым и преподнесенная в дар его патрону герцогу Фредерику фон Вюртембургу. В этом прекрасно исполненном металлическом артефакте все орбитальные сферы планет и вписанные в них правильные многогранники представляют собой не сообщающиеся между собой полые емкости, которые по праздникам предполагалось заполнять различными напитками для угощения гостей герцога.

Лишь переехав в Прагу и став ассистентом знаменитого датского астронома Тихо Браге, Кеплер натолкнулся на идеи, по-настоящему обессмертившие его имя в анналах науки. Тихо Браге всю жизнь собирал данные астрономических наблюдений и накопил огромные объемы сведений о движении планет. После его смерти они перешли в распоряжение Кеплера. Эти записи, между прочим, имели большую коммерческую ценность по тем временам, поскольку их можно было использовать для составления уточненных астрологических гороскопов (сегодня об этом разделе ранней астрономии ученые предпочитают умалчивать).

Обрабатывая результаты наблюдений Тихо Браге, Кеплер столкнулся с проблемой, которая и при наличии современных компьютеров могла бы показаться кому-то трудноразрешимой, а у Кеплера не было иного выбора, кроме как проводить все расчеты вручную. Конечно же, как и большинство астрономов его времени, Кеплер уже был знаком с гелиоцентрической системой Коперника и знал, что Земля вращается вокруг Солнца, о чем свидетельствует и вышеописанная модель Солнечной системы. Но как именно вращается Земля и другие планеты? Представим проблему следующим образом: вы находитесь на планете, которая, во-первых, вращается вокруг своей оси, а во-вторых, вращается вокруг Солнца по неизвестной вам орбите. Глядя в небо, мы видим другие планеты, которые также движутся по неизвестным нам орбитам. И задача — определить по данным наблюдений, сделанных на нашем вращающемся вокруг своей оси вокруг Солнца земном шаре, геометрию орбит и скорости движения других планет. Именно это, в конечном итоге, удалось сделать Кеплеру, после чего, на основе полученных результатов, он и вывел три своих закона!

Первый закон описывает геометрию траекторий планетарных орбит: каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. Из школьного курса геометрии - эллипс представляет собой множество точек плоскости, сумма расстояний от которых до двух фиксированных точек - фокусов - равна константе. Или иначе - представьте себе сечение боковой поверхности конуса плоскостью под углом к его основанию, не проходящей через основание, - это тоже эллипс. Первый закон Кеплера как раз и утверждает, что орбиты планет представляют собой эллипсы, в одном из фокусов которых расположено Солнце. Эксцентриситеты (степень вытянутости) орбит и их удаления от Солнца в перигелии (ближайшей к Солнцу точке) и апогелии (самой удаленной точке) у всех планет разные, но все эллиптические орбиты роднит одно - Солнце расположено в одном из двух фокусов эллипса. Проанализировав данные наблюдений Тихо Браге, Кеплер сделал вывод, что планетарные орбиты представляют собой набор вложенных эллипсов. До него это просто не приходило в голову никому из астрономов.

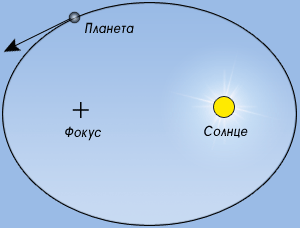
Историческое значение первого закона Кеплера трудно переоценить. До него астрономы считали, что планеты движутся исключительно по круговым орбитам, а если это не укладывалось в рамки наблюдений — главное круговое движение дополнялось малыми кругами, которые планеты описывали вокруг точек основной круговой орбиты. Это было прежде всего философской позицией, своего рода непреложным фактом, не подлежащим сомнению и проверке. Философы утверждали, что небесное устройство, в отличие от земного, совершенно по своей гармонии, а поскольку совершеннейшими из геометрических фигур являются окружность и сфера, значит планеты движутся по окружности. Главное, что, получив доступ к обширным данным наблюдений Тихо Браге, Иоганн Кеплер сумел перешагнуть через этот философский предрассудок, увидев, что он не соответствует фактам — подобно тому как Коперник осмелился убрать Землю из центра мироздания, столкнувшись с противоречащими стойким геоцентрическим представлениям аргументами, которые также состояли в «неправильном поведении» планет на орбитах.

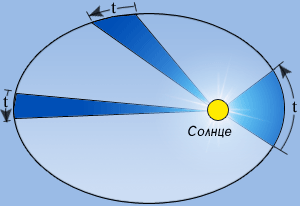
Второй закон описывает изменение скорости движения планет вокруг Солнца: каждая планета движется в плоскости, проходящей через центр Солнца, причем за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Чем дальше от Солнца уводит планету эллиптическая орбита, тем медленнее движение, чем ближе к Солнцу - тем быстрее движется планета. Теперь представьте пару отрезков, соединяющих два положения планеты на орбите с фокусом эллипса, в котором расположено Солнце. Вместе с сегментом эллипса, лежащим между ними, они образуют сектор, площадь которого как раз и является той самой «площадью, которую отсекает отрезок прямой». Именно о ней говорится во втором законе. Чем ближе планета к Солнцу, тем короче отрезки. Но в этом случае, чтобы за равное время сектор покрыл равную площадь, планета должна пройти большее расстояние по орбите, а значит скорость ее движения возрастает.

В первых двух законах речь идет о специфике орбитальных траекторий отдельно взятой планеты. Третий закон Кеплера позволяет сравнить орбиты планет между собой: квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. В нем говорится, что чем дальше от Солнца находится планета, тем больше времени занимает ее полный оборот при движении по орбите и тем дольше, соответственно, длится «год» на этой планете. Сегодня мы знаем, что это обусловлено двумя факторами. Во-первых, чем дальше планета находится от Солнца, тем длиннее периметр ее орбиты. Во-вторых, с ростом расстояния от Солнца снижается и линейная скорость движения планеты.

В своих законах Кеплер просто констатировал факты, изучив и обобщив результаты наблюдений. Если бы вы спросили его, чем обусловлена эллиптичность орбит или равенство площадей секторов, он бы вам не ответил. Это просто следовало из проведенного им анализа. Если бы вы спросили его об орбитальном движении планет в других звездных системах, он также не нашел бы, что вам ответить. Ему бы пришлось начинать все сначала - накапливать данные наблюдений, затем анализировать их и стараться выявить закономерности. То есть у него просто не было бы оснований полагать, что другая планетная система подчиняется тем же законам, что и Солнечная система.

Один из величайших триумфов классической механики Ньютона как раз и заключается в том, что она дает фундаментальное обоснование законам Кеплера и утверждает их универсальность. Оказывается, законы Кеплера можно вывести из законов механики Ньютона, закона всемирного тяготения Ньютона и закона сохранения момента импульса путем строгих математических выкладок. А раз так, мы можем быть уверены, что законы Кеплера в равной мере применимы к любой планетной системе в любой точке Вселенной. Астрономы, ищущие в мировом пространстве новые планетные системы (а открыто их уже довольно много), раз за разом, как само собой разумеющееся, применяют уравнения Кеплера для расчета параметров орбит далеких планет, хотя и не могут наблюдать их непосредственно.

Третий закон Кеплера играл и играет важную роль в современной космологии. Наблюдая за далекими галактиками, астрофизики регистрируют слабые сигналы, испускаемые атомами водорода, обращающимися по очень удаленным от галактического центра орбитам - гораздо дальше, чем обычно находятся звезды. По эффекту Доплера в спектре этого излучения ученые определяют скорости вращения водородной периферии галактического диска, а по ним - и угловые скорости галактик в целом. Труды ученого, твердо поставившего нас на путь правильного понимания устройства нашей Солнечной системы, и сегодня, спустя века после его смерти, играют столь важную роль в изучении строения необъятной Вселенной.

наверх ^

Орбиты

Большое значение имеет расчет траекторий полета космических аппаратов, в котором должна преследоваться основная цель - максимальная экономия энергии. При расчете траектории полета космического аппарата необходимо определять наиболее выгодное время и по возможности место старта, учитывать аэродинамические эффекты, возникающие в результате взаимодействия аппарата с атмосферой Земли при старте и финише, и многое другое.

Многие современные космические аппараты, особенно с экипажем, имеют относительно малые бортовые ракетные двигатели, главное назначение которых - необходимая коррекция орбиты и осуществление торможения при посадке. При расчете траектории полета должны учитываться ее изменения, связанные с корректировкой. Большая часть траектории (собственно, вся траектория, кроме активной ее части и периодов корректировки) осуществляется с выключенными двигателями, но, конечно, под воздействием гравитационных полей небесных тел.

Траектория движения космического аппарата называется орбитой. Во время свободного полета космического аппарата, когда его бортовые реактивные двигатели выключены, движение происходит под воздействием гравитационных сил и по инерции, причем главной силой является притяжение Земли.

Если считать Землю строго сферической, а действие гравитационного поля Земли - единственной силой, то движение космического аппарата подчиняется известным законам Кеплера: оно происходит в неподвижной (в абсолютном пространстве) плоскости, проходящей через центр Земли, - плоскости орбиты; орбита имеет форму эллипса или окружности (частный случай эллипса).

Орбиты характеризуются рядом параметров - система величин, определяющих ориентацию орбиты небесного тела в пространстве, ее размеры и форму, а также положение на орбите небесного тела в некоторый фиксированный момент. Невозмущенную орбиту, по которой движение тела происходит в соответствии с законами Кеплера, определяют:

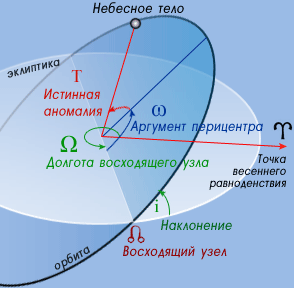
1. Наклонение орбиты (i) к плоскости отсчета; может иметь значения от 0° до 180°. Наклонение меньше 90°, если для наблюдателя, находящегося в северном полюсе эклиптики или в северном полюсе мира, тело представляется движущимся против часовой стрелки, и больше 90°, если тело движется в противоположном направлении. В применении к Солнечной системе, за плоскость отсчета обычно выбирают плоскость орбиты Земли (плоскость эклиптики), для искусственных спутников Земли за плоскость отсчета обычно выбирают плоскость экватора Земли, для спутников других планет Солнечной системы за плоскость отсчета обычно выбирают плоскость экватора соответствующей планеты.
2. Долгота восходящего узла (Ω) - один из основных элементов орбиты, используемых для математического описания формы орбиты и ее ориентации в пространстве. Определяет точку, в которой орбита пересекает основную плоскость в направлении с юга на север. Для тел, обращающихся вокруг Солнца, основная плоскость - эклиптика, а нулевая точка - Первая точка Овна (точка весеннего равноденствия).
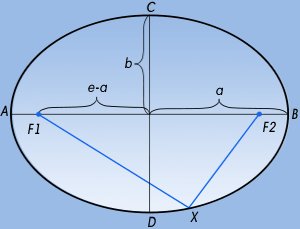
3. Большая полуось (а) - это половина главной оси эллипса. В астрономии характеризует среднее расстояние небесного тела от фокуса.
4. Эксцентриситет - числовая характеристика конического сечения. Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия и характеризует «сжатость» орбиты.
5. Аргумент перицентра - определяется как угол между направлениями из притягивающего центра на восходящий узел орбиты и на перицентр (ближайшую к притягивающему центру точку орбиты спутника), или угол между линией узлов и линией апсид. Отсчитывается из притягивающего центра в направлении движения спутника, обычно выбирается в пределах 0°-360°. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидов вокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д.
6. Средняя аномалия для тела, движущегося по невозмущенной орбите - произведение его среднего движения и интервала времени после прохождения перицентра. Таким образом, средняя аномалия есть угловое расстояние от перицентра гипотетического тела, движущегося с постоянной угловой скоростью, равной среднему движению.

Существуют различные типы орбит – экваториальные (наклонение "i" = 0°), полярные (наклонение "i" = 90°), солнечно-синхронные орбиты (параметры орбиты таковы, что спутник проходит над любой точкой земной поверхности приблизительно в одно и то же местное солнечное время), низкоорбитальные (высоты от 160 км до 2000 км), среднеорбитальные (высоты от 2000 км до 35786 км), геостационарные (высота 35786 км), высокоорбитальные (высоты более 35786 км).

наверх ^